thảo luận [Học Tập] Topic thuật toán
- Thread starter unknowpc90
- Start date
- Với thuật toán đệ quy thì tìm hiểu định lý thợ (Master theorem),
- Những thuật toán mà có hiện tượng kích thước đầu vào phải xử lý giảm cấp số nhân theo một hằng số nào đó thì thường sẽ có log(n), vì dụ cứ sau mỗi vòng lặp lại giảm 3 lần, ...
Nói chung nguyên tắc là dùng toán để đếm số phép tính cơ bản. Đương nhiên không phải lúc nào cũng làm được nên để tính O() thì có thể cho dư ra tí. Với Theta() thì cần phải chặt.
Setoid
Senior Member
Bài 2: mỗi phần tử của nums có 2 cách đặt dấu + và -
Thuật toán
Tối ưu hoá:
Độ phức tạp: trường hợp xấu nhất là không có trạng thái nào lặp lại
=> O(2^n) cho cả time và space.
Thuật toán
- sinh ra tất cả các trạng thái dùng đệ quy: 1 trạng thái gồm index của phần tử đang xét và tổng hiện tại; từ 1 trạng thái sinh ra con trái bằng phép +, sinh ra con phải bằng phép -
- không gian trạng thái là 1 cây nhị phân hoàn hảo
- nút lá là nút có index = số phần tử của nums, tại đây kiểm tra nếu tổng hiện tại = target thì số cách tăng lên 1.
Tối ưu hoá:
- ghi nhớ các nút đã sinh để tránh lặp
- nếu nút hiện tại có tổng bé hơn target thì không phải sinh nhánh con bên phải
Độ phức tạp: trường hợp xấu nhất là không có trạng thái nào lặp lại
=> O(2^n) cho cả time và space.
Ngày Được Tự Do
Senior Member
hay quá vậy, phương pháp xét các trạng thái này là gì vậy bác
Ngày Được Tự Do
Senior Member
Bài 3:
Setoid
Senior Member
Bản chất là depth-first search, kết hợp tối ưu khi có thể thôi.
Last edited:
1. Ktra độ dài mảng arr và S >=2 .
2. chia hết cho 2. Lấy len(arr) - s. Ra số bị trừ.
3. Không chia hết cho 2. Lấy (len(arr) -1)- s
4. Chia đôi mảng số bị trừ lấy đc mảng âm. Lặp mảng âm và mảng ban đầu
via theNEXTvoz for iPhone
Ngày Được Tự Do
Senior Member
Khó hiểu thế bác, số trừ và số bị trừ là gì vậy, các số ở đây không phải chỉ có 1 thui đâu nha, giá trị tuỳ
via theNEXTvoz for iPhone
trungpham90
Đã tốn tiền
2 bài fen đăng (bài 2 vs 3) đều là quy hoạch động. Ko rõ fen có học qua chưa? Nếu mới học thuật toán thì chưa nên động vào.
Bài 2 độ phức tạp là O(n*m) vs m là tổng array, còn bài 3 là O(n^4)
Last edited:
Hóng cách giải ạ
trungpham90
Đã tốn tiền
Bài 2 cách trâu bò O(n*2^n), dùng bit manipulation,
Java:
public int numberOfWays(int[]data, int sum){
int n = data.length;
int result = 0;
for(int z = 0; z < (1 << n); z++){
int total = 0;
for(int i = 0; i < n; i++){
if(((1 << i) & z) != 0){
total += data[i];
}else{
total -= data[i];
}
}
result += total == sum ? 1 : 0;
}
return result;
}
Java:
int[][][]dp;
public int numberOfWays(int []data, int sum){
int max = 1000;
dp = new int[2][data.length][max + 1];
for(int[][]a : dp){
for(int[]b : a){
Arrays.fill(b, -1);
}
}
return cal(0, 0, 0, sum, data);
}
public int cal(int index, int negative, int currentSum, int sum, int[]data){
int current = negative == 1 ? -currentSum : currentSum;
if(index == data.length){
return current== sum ? 1 : 0;
}
if(dp[negative][index][currentSum] != -1){
return dp[negative][index][currentSum];
}
int add = current + data[index];
int sub = current - data[index];
int result = cal(index + 1, add < 0 ? 1 : 0, abs(add), sum, data);
result += cal(index + 1, sub < 0 ? 1 : 0, abs(sub), sum, data);
return dp[negative][index][currentSum] = result;
}
Last edited:
nipevt
Senior Member
chương 1 CLRS thôi.
nipevt
Senior Member
giải trong O(row*col*col). Với mỗi hàng i tạo một mảng b có col phần tử, với mỗi phần tử b[j] là số hàng lớn nhất có thể đi lên từ hàng i cột j trước ghi gặp một số 0. vd cột j là:
0
1
1
thì b[j] là 2.
Chạy ngược lại và tính c= min(b[j], b[j - 1], b[ j - 2], .. b[j - k + 1])...với mỗi k như vậy cộng
Vậy cộng được thêm c hcn thỏa mãn điều kiện vào kết quả.
Last edited:
Ngày Được Tự Do
Senior Member
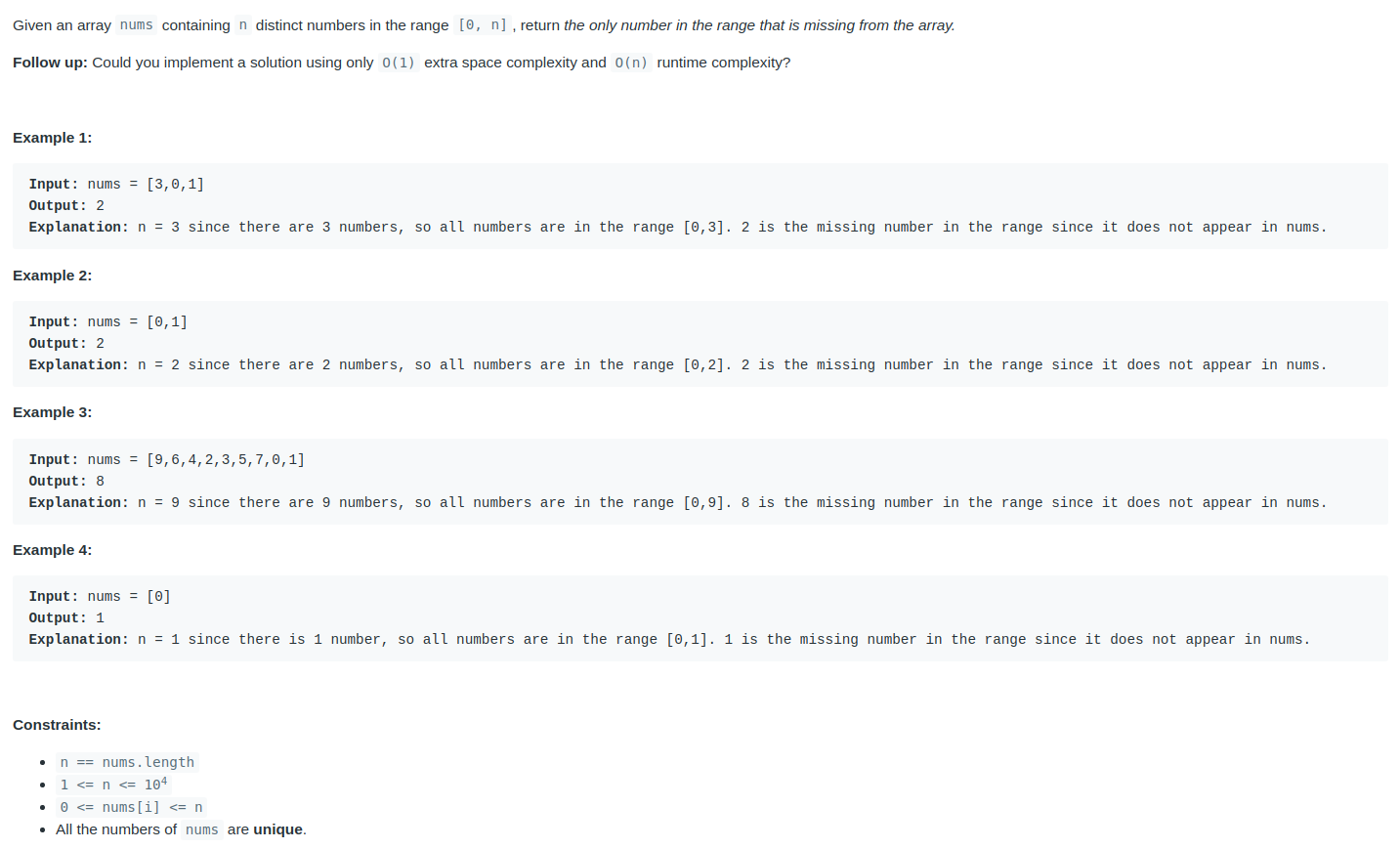
Bài 4:
Setoid
Senior Member
Bài 2 không hẳn là dynamic programming đâu; nó thiếu 2 tính chất là overlapping subproblems và optimal structure theo nghĩa của bellman. thế nên mình mới ngại gọi dp ở post trước, at best chỉ có thể gọi là recursion + memorisation, thêm ý tối ưu thứ 2 thì thêm pruning nữa là hết.
để thấy không có overlapping subproblems thì có thể ví dụ mảng đầu vào [1,2,4,8,16..,2^i] -> input kiểu này làm memoi vô dụng.
để thấy không có tối ưu thì tại mỗi bước phải bruteforce hết các lựa chọn.
Lời giải thứ 2 của thím ở trên vẫn có độ phức tạp thời gian là O(2^n) thôi (không phải O(n*m) - cái này là thành ra là bộ nhớ): có 2 lời gọi đệ quy tới cal, 1 cái dùng + tiếp bởi 1 cái dùng -
=> computation có hình dạng cây nhị phân như mình post. Bộ nhớ thì thím ấy lưu bằng mảng tốt O(n*m). còn lúc phân tích mình lưu theo cặp (index, sum).
Bài 4 thì thấy số dư = n*(n+1)/2 - Σ nums
để thấy không có overlapping subproblems thì có thể ví dụ mảng đầu vào [1,2,4,8,16..,2^i] -> input kiểu này làm memoi vô dụng.
để thấy không có tối ưu thì tại mỗi bước phải bruteforce hết các lựa chọn.
Lời giải thứ 2 của thím ở trên vẫn có độ phức tạp thời gian là O(2^n) thôi (không phải O(n*m) - cái này là thành ra là bộ nhớ): có 2 lời gọi đệ quy tới cal, 1 cái dùng + tiếp bởi 1 cái dùng -
=> computation có hình dạng cây nhị phân như mình post. Bộ nhớ thì thím ấy lưu bằng mảng tốt O(n*m). còn lúc phân tích mình lưu theo cặp (index, sum).
Bài 4 thì thấy số dư = n*(n+1)/2 - Σ nums
nipevt
Senior Member
nó là qhđ.
đề bài đã bảo tổng input dưới 1000 rồi.
cái này vẫn chưa tối ưu bộ nhớ, tối ưu nhất là lưu bằng mảng O(M) với M khoảng 2k phần tử (range giá trị từ -1000 tới 1000)
C++:
#include <bits/stdc++.h>
using namespace std;
const int N = 21;
const int M = 2003;
int dp[N][M], n, s;
void save(int i, int j, int val) {
dp[i][j + 1000] += val;
}
int get(int i, int j) {
if (j < -1000 || j > 1000) return 0;
return dp[i][j + 1000];
}
int main() {
cin >> n >> s;
vector<int> a(n);
memset(dp, 0, sizeof(dp));
for (int i = 0; i < n; ++i) cin >> a[i];
save(0, a[0], 1);
save(0, -a[0], 1);
for (int i = 1; i < n; ++i) {
for (int j = -1000; j <= 1000; ++j) {
save(i, j, get(i - 1, j + a[i]));
save(i, j, get(i - 1, j - a[i]));
}
}
cout << get(n - 1, s) << '\n';
}
Last edited:
Setoid
Senior Member
Có khác gì đâu. bác gán M, N hằng số thì số phần tử chính xác là 21*2003
bác kia gán M = 1000 và dùng mảng 3 chiều, số phần tử là 2*N*1000 <= 20*2000
(qhđ thôi không bàn)
nipevt
Senior Member
vì chỉ quan tâm i và i - 1 ở mỗi vĩ trí, nên chỉ cần lưu 2*M phần tử trong mảng 2 chiều là đủ, dp[2][M]. code trên của mình chưa tối ưu phần đó.
Ngày Được Tự Do
Senior Member
Similar threads
