thảo luận [Học Tập] Topic thuật toán

Phàm nhân tu vozer said:

Số đồ vật bằng nhau thì chỉ có TBC thôi mấy bài này cơ bản khá dễ

Click to expand...

Tuấn Mỏ said:

TBC là thuật toán j vậy thím?

Click to expand...

Tuấn Mỏ said:

TBC là thuật toán j vậy thím?

Click to expand...

Tuấn Mỏ said:

Chia sẻ bài toán xếp gạch. Bài này mình cũng không biết giải mà phải đọc cách giải thích của tác giả và nhiều nguồn khác (https://www.geeksforgeeks.org/tiling-with-dominoes/). Thấy cũng hay nên chia sẻ lại cho các vozer yêu code. Tưởng chừng rất phức tạp nhưng sau khi tìm được công thức quy hoạch động thì lại giải ra khá dễ.

Đề bài: Có 1 khu vực diện tích 3xN (3 dòng, N cột) và các viên gạch diện tích là 2x1. Tìm số cách xếp các viên gạch để lấp đầy khu vực đó.

Gọi x(n) là số cách xếp gạch full 3xN.
- TH1: Nếu ban đầu xếp viên gạch nằm dọc thì viên thứ 2 phải xếp nằm ngang chèn ở dưới, phần còn lại cần phải tìm là tìm số cách xếp gạch để lấp được khu vực 3xN-1 với 1 số khuyết. như hình dưới, tạm gọi là bài toán f(n - 1)
View attachment 829016
- TH2: Nếu ban đầu xếp viên gạch nằm ngang, thì sẽ có 2 trường hợp xảy ra tiếp theo
+ Nếu viên thứ 2 xếp nằm ngang thì viên thứ 3 cũng phải xếp nằm ngang. Vậy thì sẽ lấp đầy được diện tích 3x2 đầu tiên. Bài toàn còn lại là tìm số cách xếp gạch để lập được khu vực 3xN-2 hay gọi là x(n-2) như hình dưới
View attachment 829017
+ Nếu viên thứ 2 xếp nằm dọc thì sẽ giống với TH1. tức là f(n-1)

Từ TH1, TH2, có công thức là x(n) = x(n-2) + 2 * f(n-1)

Xét tiếp bài toán tìm số cách xếp gạch để lấp khu vực 3xN sao cho còn khuyết 1 ô

- TH3: Nếu xếp viên gạch đầu tiên nằm dọc thì phần còn lại là số cách xếp gạch sao cho đầy khu vực 3xN-1 hay là x(n-1), như hình dưới.
View attachment 829019
- TH4: Nếu xếp viên gạch nằm ngang, thì viên thứ 2 cũng phải nằm ngang. Vì nếu xếp viên thứ 2 nằm dọc thì sẽ bị sót 1 ô mà không thể lấp đc. như hình dưới
View attachment 829025
Nếu viên 1 vào viên 2 xếp ngang thì viên thứ 3 cũng phải xếp ngang, bài toàn còn lại là cách xếp để fill khu vực 3xN-2 sao cho còn khuyết 1 ô ở gốc hay f(n-2), như hình dưới.
View attachment 829028

Tứ TH3, TH4, f(n) = x(n-1) + f(n-2)

Vậy có 2 công thức là
x(n) = x(n-2) + 2f(n-1) gọi là công thức (1)
f(n) = x(n - 1) + f(n-2) gọi là công thức(2)

từ (2) => f(n - 1) = x(n-2) + f(n-3), đem thay vào (1), ta có
x(n) = x(n-2) + 2 * (x(n-2) + f(n-3) = 3 * x(n-2) + 2 * f(n-3) gọi là công thức (3)

tứ (1) => x(n-2) = x(n-4) + 2f(n-3) => 2f(n-3) = x(n-2) - x(n-4) , đem thay vào công thức (3), ta có
x(n) = 3 * x(n-2) + x(n-2) - x(n-4)
=> x(n) = 4 * x(n-2) - x(n-4)

Các trường hợp cơ bản ban đầu là
x(0) = 1, có 1 cách là ko cần xếp viên gạch nào
x(1)= 0, ko có cách nào để lấp đầy khu vực 3x1
x(2) = 3, dễ dàng tính bằng tay
x(3) = 0, ko có cách nào để lấp đầy khu vực 3x3

Chạy thuật toán bằng code

C++:

    const int N = 8;
    int X[N + 1] = { 0 };
    X[0] = 1;
    X[1] = 0;
    X[2] = 3;
    X[3] = 0;

    for (int i = 4; i <= N; ++i)
    {
        X[i] = 4 * X[i - 2] - X[i - 4];
    }

    int nRet = X[N];

tính ra nếu N= 8 thì có 153 cách.

Click to expand...

Yêu em Thu Nga CN12 ptit said:

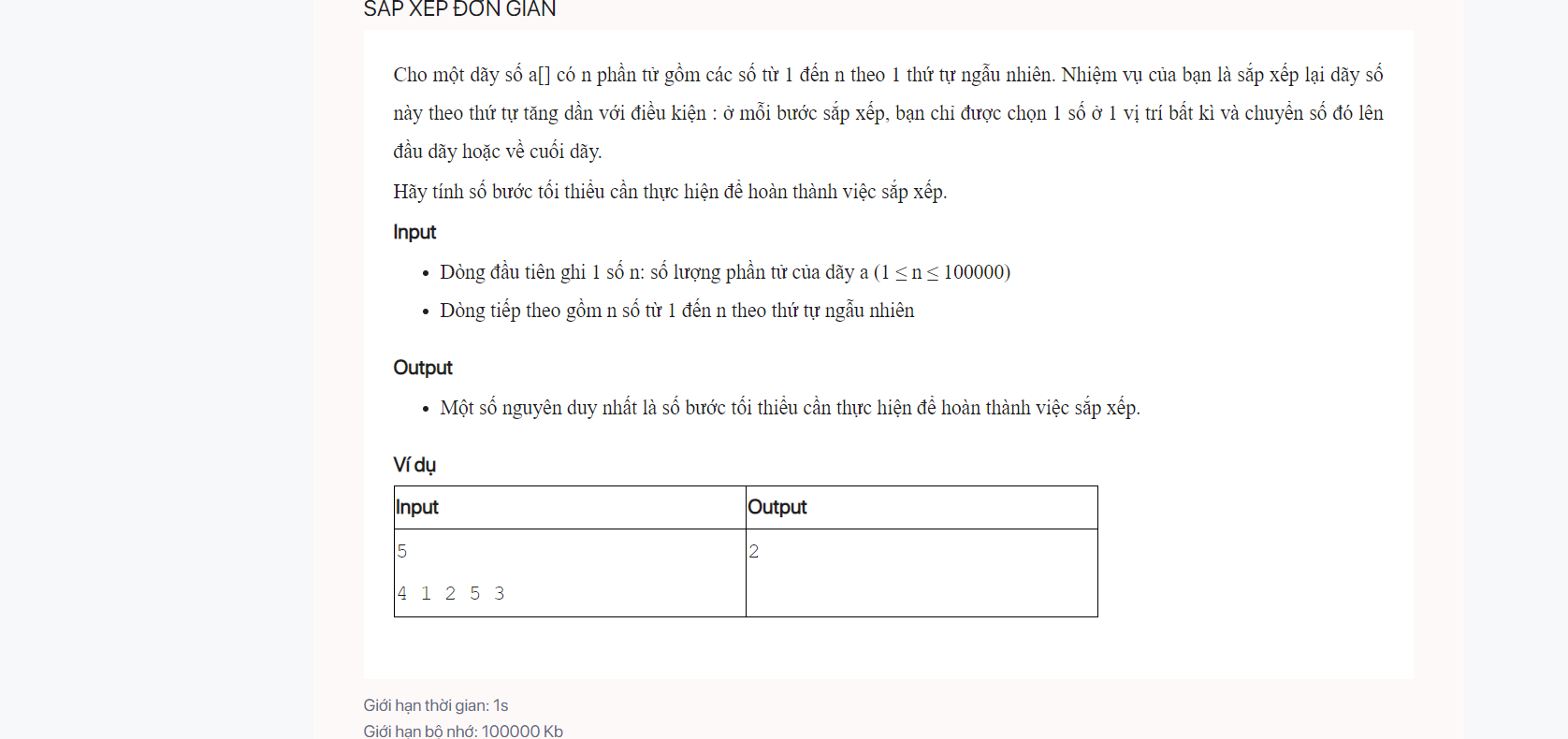
Bác nào có ý tưởng bài này không ạ? em làm kiểu tìm LIS đpt O(n^2) với chênh lệch giữa 2 phần tử là 1 rồi lấy tổng phần tử trừ đi LIS đấy thì có vẻ chuẩn nhưng bị quá time. nghĩa là phải tìm thuật O(nlogn) hoặc O(n). e đang tính LIS+binary-search để giảm đpt về O(nlogn) mà bài này thuộc phần greedy với đề có dữ liệu từ 1 đến n e chưa khai thác được nên chắc LIS không phải hướng đúng.

Click to expand...

Kân team said:

4 3 1 2 5 sao LIS đúng được

tôi thấy phải là tăng nhưng tăng bước 1 như 1 2 3 hay 3 4 5 chứ ko nhảy cóc như 1 2 5 được. Mà tăng bước 1 vậy thì có thể tính trong O(n), load vào 1 cái linked list, lướt tìm số 1, xóa 1 khỏi LL đó, tìm tiếp số 2, v.v... tới số k+1 ko thấy nữa thì có dãy 1 2 3 ... k có độ dài k. Tiếp tục tìm tiếp k+1 tới q+1, có dãy độ dài q-k, v.v... rồi tìm max độ dài của các dãy bước 1 tăng dần đó rồi lấy n trừ cho là được. Trong LL thì xóa 1 node O(1), mỗi node chỉ xóa 1 lần nên n node chỉ mất O(n) thoy

Nếu đúng thì đây là 1 trong những lần hiếm hoi cần sử dụng LL

edit: mà mỗi lần tìm k+1 trên LL lại có thể tốn O(n)

Vậy chắc dùng thêm 1 hash map lưu địa chỉ từng node trên LL nữa

edit: cũng ko được, vẫn phải tốn O(n^2) nếu dãy tăng bước 1 a..a+k có k là hằng số nhỏ, tìm dãy này mất O(n), mà có ~n/k dãy như vậy, thành ra vẫn tốn O(n^2)

à ko dùng LL nữa, dùng đại cái hash map/mảng n phần tử luôn, lưu index của từng số. Rồi tìm max độ dài dãy tăng liên tục trên cái mảng này là xong

vd 4 3 1 2 5 tạo ra cái mảng 2 3 1 0 4, (số 1 ở index 2, số 2 ở index 3, số 3 ở index 1, số 4 ở index 0, số 5 ở index 4) dãy liên tục tăng dài nhất là 2 3 có độ dài 2 lấy 5-2 là ra

Click to expand...

nashwade said:

Mình nghĩ sơ qua thì thấy LIS không đúng vì trong case 1 4 3 2 5 thì làm theo LIS bạn sẽ ra 2 nhưng kết quả là 3.

Click to expand...

NgoaiThemRoiChiecLaDa2 said:

Tôi đang không hiểu ông nói gì
À quên nói LIS thực ra nó ko hẳn LIS lắm, tôi chỉ tính kiểu increasing subsequence mà tăng dần 1 đơn vị thôi. 4 3 1 2 5 thì LIS tôi tính là (1,2) có thể (4,5). Tức là 5-2=3 là kq output. Ko biết có hướng nào làm ok hơn ko?

Click to expand...

Kân team said:

4 3 1 2 5 sao LIS đúng được

tôi thấy phải là tăng nhưng tăng bước 1 như 1 2 3 hay 3 4 5 chứ ko nhảy cóc như 1 2 5 được. Mà tăng bước 1 vậy thì có thể tính trong O(n), load vào 1 cái linked list, lướt tìm số 1, xóa 1 khỏi LL đó, tìm tiếp số 2, v.v... tới số k+1 ko thấy nữa thì có dãy 1 2 3 ... k có độ dài k. Tiếp tục tìm tiếp k+1 tới q+1, có dãy độ dài q-k, v.v... rồi tìm max độ dài của các dãy bước 1 tăng dần đó rồi lấy n trừ cho là được. Trong LL thì xóa 1 node O(1), mỗi node chỉ xóa 1 lần nên n node chỉ mất O(n) thoy

Nếu đúng thì đây là 1 trong những lần hiếm hoi cần sử dụng LL

edit: mà mỗi lần tìm k+1 trên LL lại có thể tốn O(n)

Vậy chắc dùng thêm 1 hash map lưu địa chỉ từng node trên LL nữa

edit: cũng ko được, vẫn phải tốn O(n^2) nếu dãy tăng bước 1 a..a+k có k là hằng số nhỏ, tìm dãy này mất O(n), mà có ~n/k dãy như vậy, thành ra vẫn tốn O(n^2)

à ko dùng LL nữa, dùng đại cái hash map/mảng n phần tử luôn, lưu index của từng số. Rồi tìm max độ dài dãy tăng liên tục trên cái mảng này là xong

vd 4 3 1 2 5 tạo ra cái mảng 2 3 1 0 4, (số 1 ở index 2, số 2 ở index 3, số 3 ở index 1, số 4 ở index 0, số 5 ở index 4) dãy liên tục tăng dài nhất là 2 3 có độ dài 2 lấy 5-2 là ra

Click to expand...

Kân team said:

tạo mảng p chứa index từng số rồi tìm mảng con tăng liên tục dài nhất của p thoy
code tôi viết đậm đặc lắm

C++:

int minSwaps(const std::vector<int>& v) {
    std::vector<int> p(v.size());
    int res = 0;
    for (int i : v) p[i - 1] = res++;
    for (auto it = begin(p), jt = it; it != end(p); it = jt) {
        if ((jt = std::adjacent_find(it, end(p), std::greater<int>{})) != end(p)) ++jt;
        res = std::min(res, (int)(v.size() - std::distance(it, jt)));
    }
    return res;
}

Click to expand...

    int arr[] = { 4, 1, 2, 5, 3 };

    const int N = sizeof(arr)/sizeof(int);

    int dp[N] = { 0 };

    dp[0] = 1;

    for (int i = 1; i < N; ++i)
    {
        int nMax = 0;

        for (int j = i - 1; j >= 0; --j)
        {
            if (arr[i] > arr[j])
            {
                nMax = __max(nMax, dp[j]);
                break;
            }
        }

        dp[i] = 1 + nMax;
    }

    int nRet = N - dp[N - 1];

thuyduong2007 said:

thay đổi cách tiếp cận thôi bạn, viết đệ quy thì top-down còn muốn khử đệ quy thì bottom-up.

Python:

class Solution:
    def findTargetSumWays(self, nums: List[int], target: int) -> int:
        dp = defaultdict(int)
        dp[0] = 1
        for num in nums:
            tmp_dp = dp
            dp = defaultdict(int)
            for key,value in tmp_dp.items():
                dp[key+num] += value
                dp[key-num] += value
        return dp[target]

Cách này là phiên bản khử đệ quy của cách giái trước đó của t. Tuy nhiên nó chưa thực sự tối ưu. Do nó phải tính hết toàn bộ giá trị có thể sinh ra bởi tập ban đầu. Bản chất là vét cạn thôi, nhưng do giá trị trung gian được lưu lại bởi cái dict nên giảm thiểu được việc tính toán lại. Độ phức tạp của cách này là O(2^n). Do số lượng phần tử của tập ban đầu <= 20 nên cách này k bị timeout.

Cách tối ưu hơn là chuyển về bài toán tìm số tập con có tổng bằng 1 số cho trước.
Giả sử mình có s1 là tổng của các phần tử được thêm dấu +, s2 là tổng của các phần tử được thêm dấu '-'.
s1 + s2 = sum(nums)
s1- s2 = target
=> s1 = (sum + target)/2, s2 = (sum - target)/2
bài toán quy về tìm các tập con có tổng bằng s1 hoặc s2.
Mình sẽ chọn min(s1,s2) làm giá trị cần tìm để giảm không gian tìm kiếm lại, giúp tối ưu hơn.
Ngoài ra +/- 0 thì không làm thay đổi kết quả, do đó mình sẽ đếm số lượng phần tử 0, remove ra khỏi tập ban đầu. Kết quả cuối cùng sẽ *2^numZero. (do mỗi 1 phần tử 0 thì đều có 2 cách chọn +/-). Cái này cũng giúp lời giải tối ưu hơn do giảm được số lượng phần tử cần tính.

C++:

class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        // get new target
        int sum = accumulate(nums.begin(), nums.end(), 0);
        if ((sum + target)%2 != 0 || target > sum || target < -sum) return 0;
        int s1 = (sum + target)/2;
        int s2 = (sum - target)/2;
        int new_target = min(s1,s2);
     
        //count number 0 and remove all element equal to 0
        int numZero = count(nums.begin(), nums.end(), 0);
        nums.erase(remove(nums.begin(), nums.end(), 0), nums.end());
     
     
        vector<vector<int>> dp(nums.size()+1, vector<int>(new_target + 1, 0));
        dp[0][0] = 1;
        for (int i = 0;  i < nums.size(); ++i) {
            for (int j = 0;  j <= new_target; ++j) {
                dp[i+1][j] += dp[i][j];
                if (j + nums[i] <= new_target) dp[i+1][j + nums[i]] += dp[i][j];
            }
        }
        return dp.back().back()*pow(2, numZero);
    }
};

Click to expand...

auto it = remove(nums.begin(), nums.end(), 0);
auto num_zero = nums.end() - it;
nums.erase(it,nums.end());

davinci1207 said:

DP này thì complexity vẫn là O(RxN) với R = sum(nums) thôi, tương tự như recursive with memo; bài này có lẽ không có cách giải quyết tối ưu hơn.
Góp ý nhỏ chỗ C++, vừa đếm 0 vừa bỏ 0 ra khỏi vector thì chỉ cần 1 pass:

Apache config:

auto it = remove(nums.begin(), nums.end(), 0);
auto num_zero = nums.end() - it;
nums.erase(it,nums.end());

Click to expand...

Tuấn Mỏ said:

Bác xài stl trông hầm hố quá, em xin góp 1 cách ko stl

C++:

    int arr[] = { 4, 1, 2, 5, 3 };

    const int N = sizeof(arr)/sizeof(int);

    int dp[N] = { 0 };

    dp[0] = 1;

    for (int i = 1; i < N; ++i)
    {
        int nMax = 0;

        for (int j = i - 1; j >= 0; --j)
        {
            if (arr[i] > arr[j])
            {
                nMax = __max(nMax, dp[j]);
                break;
            }
        }

        dp[i] = 1 + nMax;
    }

    int nRet = N - dp[N - 1];

Click to expand...

nashwade said:

Code thế này thì thành O(N^2) à bác

Click to expand...